Current Research Areas
- Multiphase flow instability
- Mathematical modeling for particle-wave interactions in turbulent flows and in dispersed nano-to-micron sized particle-laden flows.
- Advanced propulsion applications, solar sails, electromagnetic propulsion, Casimir forces, and vacuum fluctuations.
- Hydrodynamic – Quantum Analogs, new theories for the dynamics of particles at the microscopic scales informed by hydrodynamic stability theories.
- Turbulent reacting flows, Computational fluid dynamics, and large eddy simulations of turbulent combustion.
Multiphase flow instability and dynamics in complex flows:
We aim to synthesize theory, computations, and experiments to develop new generalized hydrodynamic stability models for multiphase flows in which chemical reactions, turbulence, and particle interactions may be involved. Situations in which the evolution of a flow and a particulate matter are strongly coupled play an important role in engineering, environmental, biological, and medical applications.
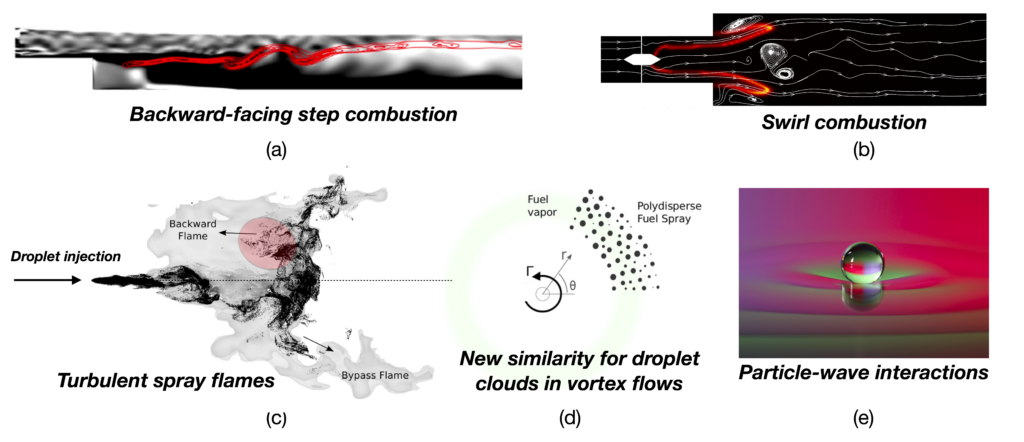
Applicative studies of the generalized stability theory for particle-laden flows: (a) Reacting shear flows of a backward-facing step configuration, in which chemical kinetics plays a crucial role in altering the hydrodynamic stability. Here, vorticity distribution is shown in black and white. (b) Swirl combustor configuration. Both reacting flow configurations exhibit highly unsteady flame (represented by CO mass fraction in red) and flow dynamics. (c) Unstable turbulent reacting spray injected into a central recirculation zone (CRZ). (d) Droplet clouds in vortex flows for which a similarity solution was found. (e) Particle wave interaction as observed in bouncing droplet experiment (Experiments conducted in the Applied mathematics laboratory at MIT).
A hydrodynamically-inspired quantum field theory and hydrodynamic quantum analogs: A hydrodinamically inspired quantum-field-theory (HQFT) was recently suggested by Dagan and Bush (Comptes Rendus Mechanique, 2020). Originally proposed by de Broglie in 1924, the particle motion is piloted by a real wave. In our model, as in the hydrodynamic quantum analog, the particle is gradient-driven. Self-excited motion and quantum statistical signatures emerge from the non-linear coupled dynamical system.
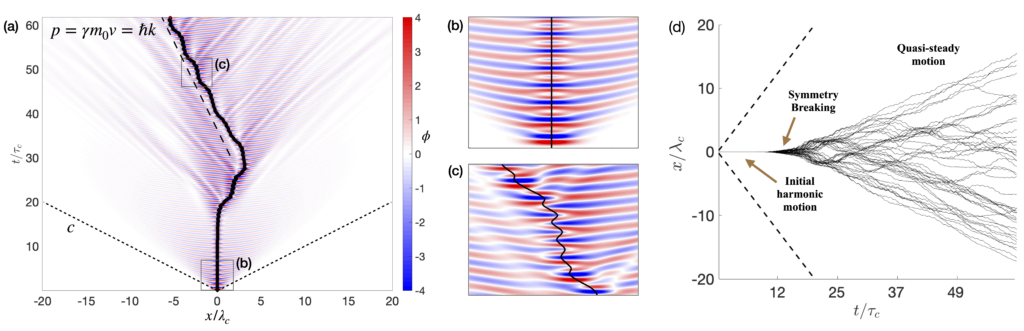
Pilot-wave dynamics of a free particle. (a) Spatio-temporal map illustrates the evolution of the normalized pilot-wave field, 𝜙, generated by the trajectory of a free particle (indicated in black). Dashed black lines correspond to 𝑝 = ħ𝑘, as calculated from the wavelength in (c), where the particle has a quasi-steady speed of approximately 0.25c. The particle’s light cone is indicated by the dotted black line with slope c. Closeup views of (b) the initial quasi-static state and (c) the subsequent quasi-steady, self-propelling state. Symmetry breaking and the emergence of self-propulsion in an ensemble of 50 free-particle trajectories is shown in (d). Dagan and Bush, Comptes Rendus Mechanique, 2020.